Extending the Real Numbers

Contents

• Introduction
• More Numbers
• Even More Numbers
• Unreal Numbers
• How Many Numbers?
• Arithmetic
• Rings and Fields
• Integer Numbers
• Visualizing the Numbers
• Multiplicative Inverses
• Extending the Numbers
• Nested Hierarchies
• Complex Numbers
• n-Dimensional Numbers
• Still Bigger Sets
• An Uncountable Hierarchy
• Loose Ends
• References

Introduction

The real numbers exist within standard arithmetic, and are conventionally designated as the set R. Our goal in this discussion is to create a set of numbers similar to the reals, having essentially all the same properties as the reals and obeying most of the same arithmetic rules. (We're assuming the usual rules and arithmetic operations over the real numbers, such as addition, multiplication, etc.)

We define a new type of number, which we'll call a suprareal, that looks and acts (almost) identical to a real number, but which is not a real itself. Furthermore, we specify that these suprareals are members of set H (the Greek letter eta), which is a set disjoint from R.

First we define how the suprareals are related to the reals. Since we want the suprareals to exist outside the range of all reals (i.e., sets H and R do not have any members in common), we do this by establishing an order relation between the suprareals and the reals:

Definition 1.
x < h for all x ∈ R and 0 < h ∈ H, and
x > h for all x ∈ R and 0 > h ∈ H.

This can be written in a slightly simpler form:

|x| < |h| for all x ∈ R and h ∈ H.

We can define set H more formally as:

Definition 2.
H⁺ = { h : h > x for all x ∈ R }.
H⁻ = { h : h < x for all x ∈ R }.
H = H⁻ ∪ H⁺.

These definitions establish the less than (<) and greater than (>) ordering relations between the suprareals and the reals, stating that the magnitude (absolute value) of every suprareal is greater than the magnitude of every real number. This guarantees that all of the suprareals lie outside the range of the reals. We state this formally in our first theorem about suprareals:

Theorem 1.
For all h ∈ H, h ∉ R.

The proof is rather obvious, since by definition any member of H has a magnitude greater than any member of R, therefore no member of H can be a member of R. In other words, no suprareal is a real. The converse of this theorem is also true:

Theorem 2.
For all x ∈ R, x ∉ H.

In other words, no real is a suprareal. The proof is essentially the same as that for Theorem 1.

At this point in the discussion, astute readers will notice that set H is empty, and that no suprareals actually exist. This is a correct observation, because there is nothing in standard arithmetic that in fact allows a suprareal to exist, i.e., there is no way to construct a number with a magnitude greater than all real numbers. So we must explicitly call suprareals into existence within our new system:

Axiom 1.
There exists η₁ such that x < η₁ for all x ∈ R.

Or, equivalently:

There exists η₁ ∈ H⁺.

This establishes the existence of a single suprareal, η₁ (eta₁), which is a member of H. It can be considered to be the "seed" or "primordial element" of the set of suprareals, providing the foundation for them in a way that is similar to the way i (√−1) provides a foundation for the imaginary numbers. For now we'll simply designate it the fundamental constant of the suprareals. (This will be discussed in more detail later on.) We won't go into any details about what the actual value of η₁ is just yet, other than to note that it is positive. Its existence alone is sufficient to continue the discussion.

Axiom 1 defines an extension to the system of standard real arithmetic. This is a key point to be remembered, because anything we say about suprareals applies only within our newly created framework, and is meaningless within the framework of standard arithmetic. In particular, we note that η₁ is a number that exists within our new system but is not a real, and thus cannot exist within standard arithmetic.

More Numbers

At this stage of the discussion, set H is pretty sparse, having the only existing suprareal to this point, η₁, as its only member. So let's add a couple of rules to allow more suprareals to exist:

Axiom 2.
For all x ∈ R, x+η₁ ∈ H.

Axiom 3.
For all x ∈ R and x ≠ 0, xη₁ ∈ H.

Now we have an entire universe of suprareals, because for each real x there are corresponding suprareals x+η₁ and xη₁. Note, however, that xη₁ is specifically excluded from being zero. The reason for this is that allowing zero as a suprareal would introduce an inconsistency with Definitions 1 and 2. To see why this is so, we introduce the next theorem:

Theorem 3.
0 ∉ H.

This is rather trivial to prove, since by Theorem 2, no member of R is a member of H, i.e., no real is a suprareal, and since 0 is a real, it cannot be a suprareal.

If we allowed 0 to be a suprareal, this theorem would be false, and 0 would be a member of H. However, this would create an inconsistency with the ordering relations of Definitions 1 and 2, which state that all suprareals are greater than (or less than) all reals, which would imply that 0 is greater than (or less than) itself. Disallowing 0 as a suprareal eliminates this contradiction.

H is populated with a lot of suprareals at this point, but the set is still not complete. We provide a couple of more axioms which allow many more suprareals to exist:

Axiom 4.
For all g ∈ H, g+η₁ ∈ H.

Axiom 5.
For all g ∈ H, gη₁ ∈ H.

These axioms lead us to two more theorems:

Theorem 4. (Partial closure under addition)
For all h,g ∈ H⁺, h+g ∈ H⁺, and
for all h,g ∈ H⁻, h+g ∈ H⁻.

This theorem states that the set of positive suprareals is closed under addition. The sum of any two members of H⁺ is always another member of H⁺. The same is true for all of the negative suprareals as well, i.e., H⁻ is closed under addition.

However, the entire set H is not closed under addition, because the sum of two suprareals could be either another suprareal or it could be a real. For example, given h = x+η₁ for some real x, and g = (−1)η₁, then h+g = x+η₁ + (−1)η₁ = x, which is a real. If it were not for these kinds of sums, all of H would be closed under addition.

Theorem 5. (Closure under multiplication)
For all h,g ∈ H, hg ∈ H.

This theorem states that the set of suprareals is closed under multiplication. This means that multiplying any two members of H results in another member of H. Multiplying suprareals always results in another suprareal, and there are no special exceptions to worry about. (We will see later that H is not a ring, but is part of a larger set that is.)

Even More Numbers

It might be tempting to think that every suprareal is either the sum of the fundamental constant η₁ and some real number (x+η₁), but this is not true. We can create a suprareal sum that is greater than any sum involving a real number:

η₁+η₁ = 2η₁ > x+η₁, for all x ∈ R.

Likewise, we can create a suprareal product that is greater than any product involving a real number:

η₁η₁ = η₁² > xη₁, for all x > 0 ∈ R.

Similarly, for any given suprareal g+η₁ or gη₁, we can create a suprareal that is larger than it:

η₁³ > gη₁ = (xη₁)η₁ = xη₁², for all g = xη₁ and x > 0 ∈ R.

In fact, it would appear that every suprareal can be represented as a polynomial over powers of η₁. This is a very important observation, so much so that we can call this the "Fundamental Theorem of Suprareals" (FTSR):

Theorem FTSR.
For all h ∈ H,
h = x + x₁η₁¹ + x₂η₁² + x₃η₁³ + ... + x_nη₁ⁿ,
where x, x₁, x₂, ..., x_n ∈ R, and at least one x_j ≠ 0.

Some examples of polynomial suprareals:

1. η₁.
2. η₁².
3. η₁¹⁸ + 1.
4. 2η₁² − 3η₁¹ + 5.
5. −³/₄η₁⁵ + ⁷/₁₆η₁³ + ⁸/₃η₁² − ⁹/₂₀.

Unreal Numbers

Since the magnitude of any given suprareal is greater than any finite real number, we could say that the suprareals must be nonfinite, or infinite numbers. But we must take care when we talk about "infinite numbers". There are various concepts of "infinity", "divergence", and "unboundedness" within mathematics, and we want to be careful about how these concepts apply to our suprareals.

Since the suprareals are designed to obey most of the rules of normal arithmetic (which we will see later), they do not behave like the infinite ordinal numbers nor the transfinite cardinal numbers of standard set theory. In particular, a given suprareal h obeys the inequality h < 1+h, which is not how an infinite ordinal or a transfinite cardinal behaves.

The term "infinite number" is an unfortunate one, and it probably makes more sense to consider the suprareals as "extremely large" numbers, or perhaps "unreal" numbers, to emphasize their relation to, and difference from, the reals. The only thing that really makes the suprareals different from the reals is the ordering relation of Definition 1. Thus it is more meaningful to think of the suprareals simply as a second set of real-like numbers that exist apart from the normal set of reals.

So we do not claim that the suprareals are infinite numbers at this point, and we want to preserve the meaning of ∞, the "usual" infinity, within our framework. We will go into more detail about this later on, but for now we simply mention this theorem in passing:

Theorem I. (Infinity)
For all h ∈ H, −∞ < h < +∞.

How Many Numbers?

We might be tempted to assume that there are more suprareals than real numbers, that H is a larger set than R. However, this is not the case.

Theorem 6.
|H| = |R|.

We prove that the two sets are the same size (or more precisely, that they have the same cardinality), first by noting that every real x (other than 0) can be mapped to a unique suprareal xη₁. This shows that |R| ≤ |H|, which we already suspected. Next we note that since each suprareal g can be represented as a polynomial over powers of η₁, we can map each g to an n-tuple of reals comprising the coefficients of the polynomial for g, which is <x₁, x₂, ..., x_n>. Furthermore, since every n-tuple of reals can be mapped one-to-one to a unique real (one way to do this is to use Cantor's method of intertwining the digits of each real in the tuple to create a single new real), it follows that every suprareal can be uniquely mapped to a single real. This shows that |H| ≤ |R|. Thus |R| = |H|. Or in other words, there are as many suprareals as there are real numbers.

Another way of looking at this is to realize that since every suprareal can be written as an n-order polynomial, the n coefficients of each suprareal are taken from Rⁿ space. And since the cardinality of every Rⁿ space is the same as the cardinality of R space, the cardinalities of H and R are likewise the same.

Arithmetic

Now we have to formalize the arithmetic operations we want to allow to apply to the suprareals. Our goal is that the suprareals behave pretty much the same under the usual arithmetic operations as the reals (possibly with a few caveats). We provide additional axioms to build upon:

Axiom 6. (Additive commutativity)
h+x = x+h, for all h ∈ H and x ∈ R.

Axiom 7. (Multiplicative commutativity)
hx = xh, for all h ∈ H and x ∈ R.

These axioms lead naturally to a few more useful theorems (which are provided without proof):

Theorem 7a. (Additive commutativity)
h+g = g+h, for all h,g ∈ H.

Theorem 7b. (Multiplicative commutativity)
hg = gh, for all h,g ∈ H.

Theorem 8a. (Additive associativity)
(h+x)+y = h+(x+y), for all h ∈ H and x,y ∈ R.

Theorem 8b. (Additive associativity)
(h+g)+x = h+(g+x), for all h,g ∈ H and x ∈ R.

Theorem 8c. (Additive associativity)
(h+g)+u = h+(g+u), for all h,g,u ∈ H.

Theorem 9a. (Multiplicative associativity)
(hx)y = h(xy), for all h ∈ H and x,y ∈ R.

Theorem 9b. (Multiplicative associativity)
(hg)x = h(gx), for all h,g ∈ H and x ∈ R.

Theorem 9c. (Multiplicative associativity)
(hg)u = h(gu), for all h,g,u ∈ H.

Theorem 10. (Additive identity)
0+h = h, for all h ∈ H.

Theorem 11. (Multiplicative identity)
1•h = h, for all h ∈ H.

Note that 0 and 1 are the additive and multiplicative identities for the suprareals, but they are not members of H themselves (because they are reals).

Theorem 12a. (Distributive law)
h(x+y) = hx+hy, for all h ∈ H and x,y ∈ R.

Theorem 12b. (Distributive law)
h(g+x) = hg+hx, for all h,g ∈ H and x ∈ R.

Theorem 12c. (Distributive law)
h(g+u) = hg+hu, for all h,g,u ∈ H.

We provide a proof of the last theorem to give some idea of how most of these are proved:

Proof 12c.
1. h = x + x₁η₁¹ + x₂η₁² + ... + x_nη₁ⁿ. (FTSR)
2. g = y + y₁η₁¹ + y₂η₁² + ... + y_nη₁ⁿ. (FTSR)
3. u = v + v₁η₁¹ + v₂η₁² + ... + v_nη₁ⁿ. (FTSR)
4. Then h(g+u) =
(x + x₁η₁¹ + x₂η₁² + ... + x_nη₁ⁿ) ((y + y₁η₁¹ + y₂η₁² + ... + y_nη₁ⁿ) + (v + v₁η₁¹ + v₂η₁² + ... + v_nη₁ⁿ)).
5. And hg+hu =
(x + x₁η₁¹ + x₂η₁² + ... + x_nη₁ⁿ) • (y + y₁η₁¹ + y₂η₁² + ... + y_nη₁ⁿ) +
(x + x₁η₁¹ + x₂η₁² + ... + x_nη₁ⁿ) • (v + v₁η₁¹ + v₂η₁² + ... + v_nη₁ⁿ).
6. Expanding (4) yields
[x(y+v) + x(y₁+v₁)η₁¹ + x(y₂+v₂)η₁² + ... + x(y_n+v_n)η₁ⁿ] +
[x₁(y+v)η₁¹ + x₁η₁¹(y₁+v₁)η₁¹ + x₁η₁²(y₂+v₂)η₁¹ + ... + x₁η₁ⁿ(y_n+v_n)η₁¹] +
[x₂(y+v)η₁² + x₂η₁¹(y₁+v₁)η₁² + x₂η₁²(y₂+v₂)η₁² + ... + x₂η₁ⁿ(y_n+v_n)η₁²] +
... +
[x_n(y+v)η₁ⁿ + x_nη₁¹(y₁+v₁)η₁ⁿ + x_nη₁²(y₂+v₂)η₁ⁿ + ... + x_nη₁ⁿ(y_n+v_n)η₁ⁿ].
7. Expanding (5) yields the same as (6).
8. Thus h(g+u) = hg+hu.

We note that additive inverses and subtraction are also defined over the suprareals:

Theorem 13. (Additive inverse)
For all h ∈ H, −h exists such that −h + h = 0.

Theorem 14. (Subtraction)
h−g = h + −g, for all h,g ∈ H.

Some example equations involving suprareals:

1. (4η₁² + η₁¹ − 5) + (−2η₁³ − 3η₁¹ + 6) = (−2η₁³ + 4η₁² − 2η₁¹ + 1).
2. (η₁² + ¹⁵/₈η₁¹ − ³/₂) + (−¹/₂η₁² + ³/₄η₁¹ + ³/₅) = (−¹/₂η₁² + ²¹/₈η₁¹ − ⁹/₁₀).
3. (3η₁² + 2) • (η₁¹ − ¹/₂) = (3η₁³ − ³/₂η₁² + 2η₁¹ − 1).

Rings and Fields

As mentioned earlier, Theorems 4 and 5 state that the suprareals are almost closed under addition and multiplication. Axioms 6 and 7 state that addition and multiplication are also commutative operations. Theorem 12c further states that these operations are distributive as well. Theorem 13 defines additive inverses for the suprareals. With all of these properties, the positive suprareals and the negative suprareals almost form commutative rings, (H⁺, +, •) and (H⁻, +, •). However, because the additive and multiplicative identities (0 and 1) are not members of H⁺ or H⁻, this prevents them from forming rings.

Also recall that there are exceptional cases where adding suprareals results in reals, which prevents the entire set of suprareals H from forming a commutative ring. However, since suprareal sums are either suprareals or reals, and the additive and multiplicative identities 0 and 1 are reals, we can combine the suprareals and the reals into a set that is completely closed under addition and multiplication:

Theorem 15a. (Closure under addition)
For all h,g ∈ H ∪ R, h+g ∈ H ∪ R.

Theorem 15b. (Closure under multiplication)
For all h,g ∈ H ∪ R, h•g ∈ H ∪ R.

Theorem 15c. (Additive identity)
For all h ∈ H ∪ R, 0 ∈ H ∪ R and 0+h = h.

Theorem 15d. (Multiplicative identity)
For all h ∈ H ∪ R, 1 ∈ H ∪ R and 1•h = h.

Theorem 15e. (Additive inverse)
For all h ∈ H ∪ R, −h ∈ H ∪ R and −h + h = 0.

This means that the combined set H ∪ R is a ring:

Theorem 16.
(H ∪ R, +, •) is a commutative ring.

The reals also form a field, which means that they form a ring that is closed under the division operation, or more precisely, that every real except zero has a multiplicative inverse. We have not defined division or multiplicative inverses for the suprareals, however, so (H ∪ R, +, •) is not a field. (Later we will see that it is part of a larger set that is, though.)

Integer Numbers

If we restrict the coefficients of each suprareal polynomial to the integers, we get a subset of the suprareals that act something like real integers. That is, each suprareal that is a polynomial with integer coefficients over powers of η₁ is something we can call a suprainteger:

Definition 3.
suprainteger p = k + k₁η₁¹ + k₂η₁² + ... + k_nη₁ⁿ,
where k, k₁, k₂, ..., k_n ∈ Z, and at least one k_j ≠ 0.

For convenience, we place these numbers into their own set H_I, which is a subset of H:

Definition 4.
H_I = { p : p is a suprainteger }.

Like the suprareals, the supraintegers are almost closed under addition and are completely closed under multiplication:

Theorem I-1. (Partial closure under addition)
For all p,q ∈ H_I⁺, p+q ∈ H_I⁺, and
for all p,q ∈ H_I⁻, p+q ∈ H_I⁻.

Theorem I-2. (Closure under multiplication)
For all p,q ∈ H_I, pq ∈ H_I.

While H_I⁺ and H_I⁻ are closed under addition and multiplication, the additive and multiplicative identities 0 and 1 are not members of either set. In addition, H_I is not completely closed under addition, because some supraintegers sums are reals. However, combining set H_I with the integers produces a set that is completely closed under addition and multiplication:

Theorem I-3. (Additive closure)
For all p,q ∈ H_I ∪ Z, p+q ∈ H_I ∪ Z.

Theorem I-4. (Additive identity)
For all p ∈ H_I ∪ Z, 0 ∈ H_I ∪ Z and 0+p = p.

Theorem I-5. (Multiplicative identity)
For all p ∈ H_I ∪ Z, 1 ∈ H_I ∪ Z and 1•p = p.

The combined set is therefore a ring:

Theorem I-6.
(H_I ∪ Z, +, •) is a commutative ring.

A few examples of supraintegers arithmetic:

1. η₁ + η₁ = 2η₁.
2. 2η₁ + 3η₁ = 5η₁.
3. (−7η₁³ − 4η₁² + 1) + (2η₁² + 11η₁¹ − 9) = −7η₁³ − 2η₁² + 11η₁¹ − 8.
4. 8η₁² + −8η₁² = 0.
5. 2η₁ • 3η₁ = 6η₁².
6. (−7η₁³ − 4η₁² + 1) (2η₁² + 11η₁¹ − 9) = −14η₁⁵ − 85η₁⁴ − 107η₁³ + 38η₁² + 11η₁¹ − 9.

The simplest subset of supraintegers are the "counting" suprareals:

Definition 5.
p = k+η₁, for all k ∈ Z.

This defines the sequence:

..., −3+η₁, −2+η₁, −1+η₁, η₁, 1+η₁, 2+η₁, 3+η₁, ...

An interesting thing to notice about this sequence is that there is no least positive suprainteger:

Theorem I-7.
k+η₁ > 0, for all k ∈ Z.

This is a direct consequence of the more general fact that there is no least positive suprareal. Likewise, there is no largest negative suprainteger:

Theorem I-8.
k−η₁ < 0, for all k ∈ Z.

These observations are of importance to the next section.

Visualizing the Numbers

It is easy to visualize the set of real numbers R as a continuous line (the "real number line"), centered at zero and extending infinitely far to the right through the positive reals and infinitely far to the left through the negative reals.

Visualizing the set of suprareals H is a little trickier, however, because even though the suprareals act like real numbers in almost every respect, they do not form a single contiguous set. More precisely, the positive suprareals (H⁺) are separated from the negative suprareals (H⁻) by a kind of "gap". This can be seen by starting on the positive suprareal line at η₁ and moving progressively to the left by repeatedly subtracting 1, and noting that there is no least positive suprareal. By the same token, start on the negative suprareal line at −η₁ and moving progressively to the right, repeatedly adding 1, and note that there is no greatest negative suprareal. This is formalized in these simple theorems (which are generalizations of Theorems I-7 and I-8, and are direct consequences of Axiom 2):

Theorem 17a.
For all h ∈ H⁺, h−1 ∈ H⁺.

Theorem 17b.
For all h ∈ H⁻, h+1 ∈ H⁻.

In other words, there is no point where the negative suprareals "meet" the positive suprareals. In fact, not only do the two half-sets not meet, there is a large gap separating them, as large as the entire real number line. Remember that all positive suprareals are greater than all the reals, and likewise all negative suprareals are less than all the reals (by Definitions 1 and 2).

So we're left with a split number line, with the right half containing the positive suprareals and the left half containing the negative suprareals. To form a visualization that makes sense, we mark the fundamental constant +η₁ on the positive half and −η₁ on the negative half. These are the "center points" for the two suprareal half-sets.

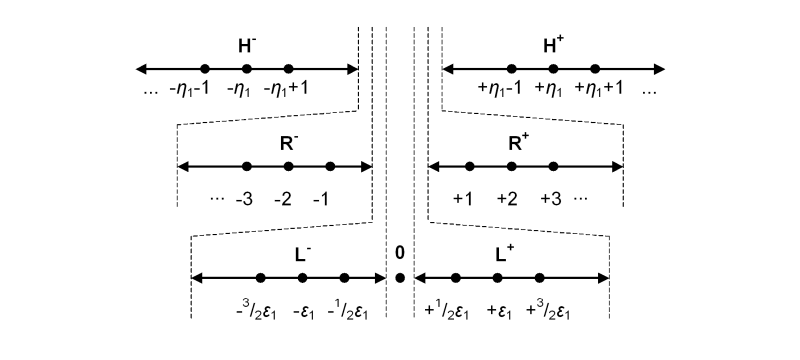
Combining the two sets R and H gives us an extended number line with zero in the center. In other words, we can fit the real number line between the halves of the suprareal line, capturing the essence of the ordering relationship between the negative suprareals, the reals, and the positive suprareals.

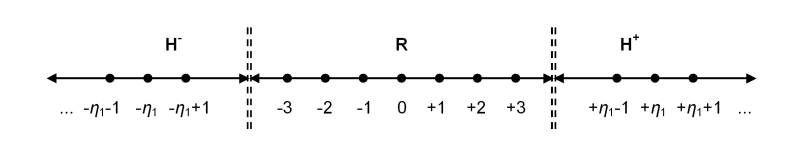
As useful as this diagram is, it's important to realize that visualizing the union of the reals and the suprareals (R ∪ H) as a single contiguous extended real number line is misleading, because there is no continuity or "connecting points" between the negative reals and the negative suprareals, and likewise none between the positive reals and the positive suprareals. No matter how far to the right we proceed along the positive reals, we never reach a "greatest positive" real that is adjacent to a "least positive" suprareal. There is no point where the reals "meet" the suprareals, on either the positive or the negative half of the lines. Thus the union of the two sets contains two "gaps", or discontinuities, between them.

Multiplicative Inverses

Earlier it was implied that defining multiplicative inverses (a reciprocal or division operator) over the suprareals could possibly make them a field. This is not quite correct; what happens is that once multiplicative inverses are introduced into our system, a new kind of number is brought into existence. Given any real x greater than 1, its reciprocal ¹/_x is a positive real number less than 1 but greater than 0. Similarly, given any positive suprareal h, which by definition is greater than any real, its reciprocal ¹/_h is a new positive number that is less than any real but still greater than 0. We formalize this with an axiom that defines into existence a specific multiplicative inverse of the suprareals:

Axiom 8.
There exists ε₁ = ¹/_η1, such that 0 < ε₁ < x for all x ∈ R.

For all h ∈ H where h > 0, there exists ε = ¹/_h,
such that 0 < ε < x for all x ∈ R.

This new fundamental constant ε₁ and all the other numbers derivable from it are infinitesimal numbers, because they are smaller than any real but still greater than zero. For now, however, we'll simply call them the i-suprareals ("inverse suprareals"). For convenience, we place them into their own set L:

Definition 6.
L = { ¹/_h : h ∈ H }.

Like the suprareals, it appears that every i-suprareal can be represented as a polynomial over powers of ε₁:

Theorem FTI.
For all v ∈ L,
v = x₁ε₁¹ + x₂ε₁² + x₃ε₁³ + ... + x_nε₁ⁿ,
where x₁, x₂, ..., x_n ∈ R, and at least one x_j ≠ 0.

As was noted earlier, the suprareals by themselves are not a field (because dividing a suprareal by some other number does not always produce another suprareal), but the union of the suprareals, the reals, and the i-suprareals is indeed a field:

Theorem 18a. (Closure over addition)
For all u,v ∈ H ∪ R ∪ L, u+v ∈ H ∪ R ∪ L.

Theorem 18b. (Closure over multiplication)
For all u,v ∈ H ∪ R ∪ L, u•v ∈ H ∪ R ∪ L.

Theorem 18c. (Closure over multiplicative inversion)
For all u ≠ 0 ∈ H ∪ R ∪ L, ¹/_u ∈ H ∪ R ∪ L.

Theorem 18d. (Additive identity)
For all u ∈ H ∪ R ∪ L, 0+u = u.

Theorem 18e. (Additive inverse)
For all u ∈ H ∪ R ∪ L, −u + u = 0.

Theorem 18f. (Multiplicative identity)
For all u ∈ H ∪ R ∪ L, 1•u = u.

Theorem 18g. (Multiplicative inverse)
For all u ≠ 0 ∈ H ∪ R ∪ L, u•¹/_u = 1.

Theorem 19.
(H ∪ R ∪ L, +, •) is a field.

To visualize adding the i-suprareals to the extended real number line, note that all of the positive i-suprareals fall between zero and all of the positive reals, and likewise for the negative i-suprareals, which fall between all of the negative reals and zero. So if we visualize the normal real number line as being centered at zero, we can split it into two half-lines and a point, i.e., the negative reals, zero, and the positive reals.

The negative i-suprareals are then inserted between the negative half-line and zero, and the positive i-suprareals are inserted between zero and the positive half-line. Positive and negative ε₁ are used as the "center points" of the i-suprareal half-lines.

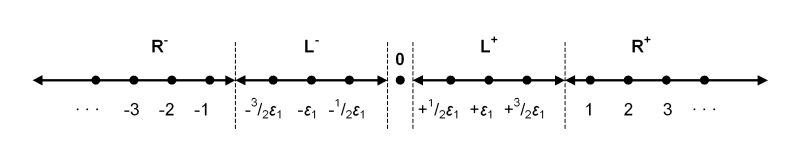
We can now show the hierarchy of i-suprareals, reals, and suprareals by listing their half-lines according to the ordering of the points contained within them:

For all positive ε ∈ L, x ∈ R, h ∈ H,
−∞ < −h < −x < −ε < 0 < +ε < +x < +h < +∞

H⁻ < R⁻ < L⁻ < 0 < L⁺ < R⁺ < H⁺

Extending the Numbers

The visualization shown earlier of the reals nested within the suprareals suggests that we can continue to extend the suprareals even further, adding another layer of numbers surrounding the suprareals. If we call the suprareals as they have been defined earlier as η₁-numbers, we can likewise define new η₂-numbers into existence. To make things a little clearer, we'll rename set H as H₁, since it is composed of all the η₁-numbers derived from η₁.

Just as we defined a fundamental element η₁ which is greater than any real number, likewise we now define another fundamental element η₂ which is greater than any η₁-number (and which is obviously greater than any real number as well):

Axiom 9.
There exists η₂ ∈ H₂ such that g < η₂ for all g ∈ H₁.

All the new suprareals derived from the fundamental constant η₂ are contained in the new set H₂.

We can continue defining more layers of suprareals indefinitely, defining into existence an entire hierarchy of suprareals:

Axiom 9. (Generalized)
There exists η_i+1 ∈ H_i+1 such that g < η_i+1 for all g ∈ H_i.

It appears that each higher level of suprareals can be represented as polynomials over powers of the fundamental η_i for that level:

Theorem G-FTSR.
For all g ∈ H_i, g = u + u₁η_i¹ + u₂η_i² + u₃η_i³ + ... + u_nη_iⁿ,
where u, u₁, u₂, ..., u_n ∈ H_i−1, and at least one u_j ≠ 0.

All of the H_j sets together form a nested hierarchy of suprareals, where the positive and negative halves of each set H_j encloses set H_j−1, forming a nested grouping all the way down to H₁, which encloses R.

Earlier we defined a fundamental i-suprareal constant ε₁ corresponding to the fundamental suprareal η₁, and likewise we can define an entire hierarchy of sub-infinitesimals ε_i corresponding to each η_i.

Axiom 10.
There exists ε_i+1 = ¹/_ηi+1, such that 0 < ε_i+1 < ε_i.

For all g_i ∈ H_i⁺ there exists ε_i = ¹/_gi,
such that 0 < ε_i < ε_i−1 < x, for all g_i−1 ∈ H_i−1⁺ for all x ∈ R.

All inverse suprareals can be expressed as polynomials over powers of ε_i:

Theorem G-FTI.
For all g ∈ L_i, g = v + v₁ε_i¹ + v₂ε_i² + v₃ε_i³ + ... + v_nε_iⁿ,
where v, v₁, v₂, ..., v_n ∈ L_i−1, and at least one v_j ≠ 0.

All of the suprareal sets and i-suprareal sets can be collected together into a single set. This single mega-set, combined with the real numbers, contains all of the reals, all of the suprareals, and all of the i-suprareals:

Definition 7.
R_E = R ∪ H₁ ∪ L₁ ∪ H₂ ∪ L₂ ∪ ...

R_E is the set of "extended reals", and contains all of the numbers, real and non-real, defined in our system.

Nested Hierarchies

Up to this point, we've defined suprareal fundamental constants η_i and their corresponding inverse suprareal constants ε_i = ¹/_ηi. But we have not defined an η₀. Since the suprareals in H_i form a hierarchy greater than the reals, and the inverse suprareals L_i form a hierarchy less than the reals, it seems logical to conclude that we can define H₀ to be the set of reals, R. Thus:

Theorem 20. (H₀)
H₀ = L₀ = R.

Since H₋₀ is simply H₀, L₀ is just another name for H₀, which is just another name for R. Furthermore, since η₀ is the fundamental constant of H₀, and since its reciprocal ¹/_η0 is the fundamental contant of L₀, and both of these sets are actually the same set R, it follows that η₀ is its own inverse in R. That is to say:

Theorem 21. (η₀)
η₀ = ¹/_η0 = 1.

Given all of this, we can simplify our notation somewhat by renaming each set L_i as its equivalent set H_−i. So where each set H_i has a fundamental contant η_i, likewise each set H_−j has a fundamental contant η_−j = ε_j = ¹/_ηj. This makes the set names L_j redundant, as we now can consider every suprareal, inverse suprareal, or real as a member of some suprareal set H_i.

[This may require some adjustments to the notion that 0 and 1 are not "proper" suprareals, since they are not members of any set H_i where i ≠ 0, but they are members of H₀. Taken as a whole, the union of all H_i sets is therefore a field and a "complete" superset of R.]

Complex Numbers

We can go another step further and extend the suprareals over the complex field. Just as a complex real number is a combination of real and imaginary parts, a complex suprareal is likewise a combination of suprareal and imaginary suprareal parts:

Definition 8.
z = u + iv, for some u,v ∈ H₁.

Applying this to the entire hierarchy of suprareals, for every suprareal and i-suprareal set H_i there is a corresponding set CH_i that extends those suprareals into the complex plane:

Definition 9.
CH_i = { z : z = u+iv for all u,v ∈ H_i } for all i ∈ Z.

Note that as a special case CH₀ is just C, the standard set of complex numbers.

The final step is to combine all of the complex suprareals, complex i-suprareals, and complex reals into a single set, the extension of the complex numbers:

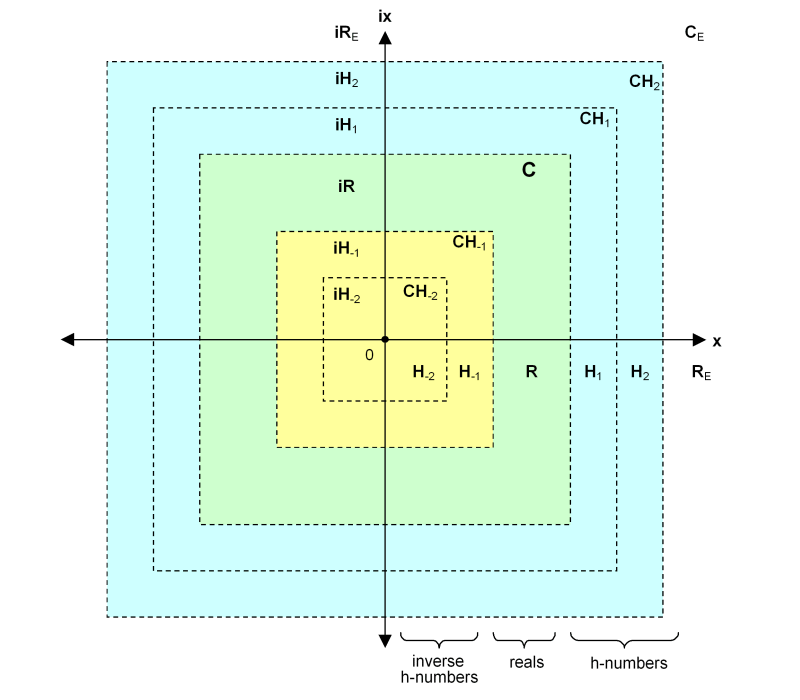
Definition 10.
C_E = C ∪ CH₁ ∪ CH₋₁ ∪ CH₂ ∪ CH₋₂ ∪ ...

The diagram below illustrates one way of visualizing set C_E. The dashed lines represent the discontinuities between the subsets comprising the extended complex plane. The diagram is simplified, showing only two levels of suprareals and i-suprareals instead of the entire (infinite) hierarchy.

n-Dimensional Numbers

We can also extend the suprareals into quaternion space, creating numbers of the form ih+jg+ku.

Our final step is to extend the suprareals into n-dimensional number spaces. The approach is to define n-tuples <v₁, v₂, v₃, ...>, where each v_i is a member of R_E or C_E.

Still Bigger Sets

If we consider that zero is surrounded by the entire set of i-suprareals, the negative i-suprareals on the left and the positive i-suprareals on the right, we could say that the i-suprareals form a "cloud" or "halo" (borrowing a term from non-standard analysis ^[2]) of non-real numbers around zero.

Taking this concept one step further, we can combine the i-suprareals with all of the reals in such a way that every real is surrounded by its own halo of i-suprareals:

Definition 11.
R_L = R ∪ { x+ε : x ∈ R and ε ∈ L }.

Or, equivalently:

R_L = { x+ε : x ∈ R and ε ∈ {0} ∪ L }.

This defines set R_L having all the reals as members, and for each real x, all of the i-suprareals x+ε surrounding x as well.

We can likewise define a set of the suprareals that includes the i-suprareal halos around each suprareal:

Definition 12.
H_L = H ∪ { h+ε : h ∈ H and ε ∈ L }.

Since the i-suprareals are defined in terms of the fundamental constant ε₁, which in turn is defined in terms of the fundamental constant η₁, we can rewrite the i-suprareals as polynomials over negative powers of η₁ (where ε₁ⁿ = ¹/_η1ⁿ = η₁⁻ⁿ):

For all v ∈ L,
v = x₁η₁⁻¹ + x₂η₁⁻² + ... + x_nη₁⁻ⁿ,
where x₁, x₂, ..., x_n ∈ R, and at least one x_j ≠ 0.

Furthermore, the members of H_L are sums of suprareals and i-suprareals. It is therefore apparent that the members of this new set can be described as polynomials over all of the integral powers of η₁ (positive and negative powers included):

Theorem FTSR-L.
For all h ∈ H_L,
h = y_mη₁^−m + ... + y₂η₁⁻² + y₁η₁⁻¹ + x + x₁η₁¹ + x₂η₁² + ... + x_nη₁ⁿ,
where y_m, ..., y₂, y₁, x, x₁, x₂, ..., x_n ∈ R, and at least one x_j ≠ 0.

And finally, we can combine all of these numbers with the infinitesimals into a single set:

Definition 13.
R_U = L ∪ R_L ∪ H_L.

Every element in this set is either a real or a suprareals, an i-suprareal, a real plus an i-suprareal, or a suprareal plus an i-suprareal.

An Uncountable Hierarchy

Up to this point, we have defined a countable hierarchy of suprareals and inverse suprareals, i.e., the sets H_n for every integer n. (Remember that H₀ is a special case and is the same as R.)

But we can create an uncountable hierarchy of suprareal sets by defining an suprareal constant for every real:

Axiom 9-U. (Generalized uncountable)
For all x ∈ R and x > 0,
there exists η_x ∈ H_x such that r < η_x for all r ∈ R,
and η_x < η_y for all x,y ∈ R where x < y.

Axiom 10-U. (Generalized uncountable)
For all η_x ∈ H_x,
there exists ¹/_ηx = ε_x ∈ H_−x such that 0 < ε_x < r for all r ∈ R.

In other words, for every real x there is a suprareal η_x, which is the fundamental constant for an entire set of suprareals H_x. Every suprareal h in H_x can be written as a polynomial over integer powers of η_x, thus h = f(η_x). Furthermore, for every suprareal h_x in H_x and every suprareal h_y in H_y, h_x < h_y when x < y.

For example, we can compare various suprareals:

h = f_h(η₁) = x₀ + x₁η₁¹ + x₂η₁² + ... + x_kη₁^k
g = f_g(η_0.5) = y₀ + y₁η_0.5¹ + y₂η_0.5² + ... + y_mη_0.5^m
u = f_u(η_π) = z₀ + z₁η_π¹ + z₂η_π² + ... + z_nη_πⁿ

Since 0.5 < 1 < π, we know that η_0.5 < η₁ < η_π, which tells us that f_g(η_0.5) < f_h(η₁) < f_u(η_π), and therefore g < h < u.

We can combine all of the H_x sets into a single set:

Definition 14.
H_R = { h : h ∈ H_x } for all x ∈ R.

Or, equivalently:

H_R = ∪ H_x for all x ∈ R.

Since |R| = c, and since |H_x| = c for every for each real x in R, there are c² suprareals in the union of all the H_x sets. By cardinal exponentiation, c² = c, so |∪H_x| = c. In other words, H_R is the same size as R and H.

Loose Ends

The definition of the suprareals could be simpler. In particular, there seem to be too many axioms, which could probably be replaced by a more general rule, something like the transfer principle ^[4] of non-standard analysis ^[2], which would allow most of the arithmetic operators (order, addition, and multiplication) to be defined over the suprareals with a single rule. In particular, Axiom 6 (additive commutativity) and Axiom 7 (multiplicative commutativity) should be theorems instead of axioms.

There is also the question of how operations more complex than arithmetic addition and multiplication may be defined over the suprareals. Analytic functions require the notion of limit, and it is not yet clear how lim_h→∞ f(h) is to be defined for h in H.

Are the suprareals the same as the hyperreals ^[1] of non-standard analysis? They certainly share some of the same properties, notably their ordering relation to the reals. It could be that a given member of R_L, being the sum of a real and an i-suprareal x+ε, is equivalent to a non-standard real r and one of the infinitesimals in its halo, with x being the standard part of r, thus x = st(r) and ε = r − st(r).

In other ways, though, the suprareals do not appear to behave like the hyperreals. Specifically, the infinite set of standard real numbers is not definable within internal set theory ^[5] (specifically, all infinite sets of IST contain a non-standard element, and all sets of IST containing only standard elements are always finite), yet R is clearly definable as a proper subset of R_E and R_L. Also, the hyperreals *R do not form a metric space, but it appears that the suprareal sets H, R_E, and L ∪ R_L ∪ H_L do.

Furthermore, reciprocals of non-standard infinitesimals are called infinite numbers (because they are larger than any reals), whereas the suprareals, while also being reciprocals of infinitesimals, are not considered to be numbers with infinite magnitudes, but simply comprise a different set of numbers similar to, but separate from, the reals. This could be just a difference in nomeclature, though, if it turns out that the suprareals and the hyperreals are equivalent. The hyperreals are also called illimited numbers, which is probably the more "correct" term.

Another issue to discuss in more detail is the fact that each region (or level) of suprareals is unconnected to any other region. For example, each h = xη_i is greater than every g = y+η_i (for positive reals x,y). Furthermore, each h in H_i is greater than every g in H_i−1. All of these suprareals exist within different, unconnected regions of suprareal space. The suprareals form a highly unconnected set, in fact.

The author does not posess the mathematical expertise to answer these questions definitively, so perhaps others with a deeper understanding of these things can provide better answers.

References

[1] Hyperreal numbers

Wikipedia: http://en.wikipedia.org/wiki/Hyperreal_number,
MathWorld: http://mathworld.wolfram.com/HyperrealNumber.html.

[2] Nonstandard Analysis

Wikipedia: http://en.wikipedia.org/wiki/Nonstandard_analysis,
MathWorld: http://mathworld.wolfram.com/NonstandardAnalysis.html.

[3] Nonstandard Analysis

Abraham Robinson, 1974, ISBN 0-691-04490-2.

[4] Transfer Principle

Wikipedia: http://en.wikipedia.org/wiki/Transfer_principle,
MathWorld: http://mathworld.wolfram.com/TransferPrinciple.html.

[5] Internal Set Theory

Wikipedia: http://en.wikipedia.org/wiki/Internal_set_theory,
MathWorld: http://mathworld.wolfram.com/SaturatedEnlargement.html.

This document: http://david.tribble.com/text/hnumbers.html.

Copyright ©2006 by David R. Tribble, all rights reserved.
Permission is granted to reference, quote, and link to this document provided that appropriate credit is given to the orginal author.